Существующие методы выявления аномалий телетрафика в мультисервисных сетях.
Для начала введем основные понятия из теории телетрафика. Телетрафик – это понятие, которое можно определить как движение информационных потоков в информационных системах. Теория телетрафика изучает закономерности и количественное описание информационных потоков. Основной математической моделью процессов, описывающих трафик в телекоммуникационных сетях, является случайный поток данных.
Аномалией в телетрафике будем называть нетипичный трафик в сети передачи данных, который приводит к проблемам в передаче данных, а именно, может блокировать работу сети и ее компонентов. Также, под аномалией в телетрафике будем подразумевать доступ к информации, которая противоречит законодательной базе и иным нормативным актам и концепциям обеспечения национальной безопасности.
Мы остановимся на вопросе выявления аномалий.
Для освещения существующих методов выявления аномалий в телетрафике, мы будем опираться на существующую теорию телетрафика и известные математические модели описывающие трафик в телекоммуникационных сетях.
Выявление аномалий на основании статистических свойств телетрафика.
Основной математической моделью процессов, описывающих трафик в телекоммуникационных сетях, является случайный поток данных. Случайный поток обладает следующими основными свойствами:
- стационарность – независимость вероятностных характеристик от времени;
- степень последействия – уровень зависимости вероятности поступления событий от предыдущих;
- ординарность – бесконечно малая вероятность поступления более одного события за бесконечно малый интервал времени.
Многочисленные современные исследования Интернет трафика свидетельствуют о том, что он обладает свойством самоподобия.
Простейшим самоподобными объектами являются фракталы. Согласно определению Мандельброта:
- «фрактал – структура, состоящая из частей, которые в каком-то смысле подобны целому».
- Неформально — самоподобный процесс определяетcя как случайный процесс, статистические характеристики которого проявляют свойства масштабирования.
В отличие от пуассоновских процессов, самоподобные характеризуются наличием последействия: вероятность поступления следующего (очередного) события зависит не только от времени, но и от предыдущих событий (предыстории). Это означает, что число текущих событий может зависеть от числа предыдущих событий в отдаленные промежутки времени. Поэтому одним из основных свойств самоподобного процесса является медленно убывающая зависимость.
Важнейшим параметром, характеризующим степень самоподобия, является параметр Херста H, определяемый для временного ряда Xk,k=1,2,K N из соотношения
где
- R=max(Xk) — min(Xk) — размах отклонения;
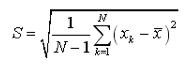 — стандартное отклонение,
— стандартное отклонение, - N — число членов временного ряда, а — константа.
Используя значение показателя Херста H, выделяют три типа случайных процессов:
- 0<=H<=0,5 — случайным процесс является антиперсистентным, или эргодическим, рядом, который не обладает самоподобием;
- H = 0,5 — полностью случайный ряд, аналогичный случайным смещениям частицы при классическом броуновском движении;
- H > 0,5 — персистентный (самоподдерживающийся) процесс, который обладает длительной памятью и является самоподобным.
Дополнительно следует отметить, что самоподобный процесс часто носит взрывной характер, что выражается в возможности наличия выбросов во время относительно низкой скорости поступления событий.
Применительно к трафику самоподобие выражается в неизменности поведения при изменении временных масштабов наблюдения и сохранения склонности к всплескам при усреднении по шкале времени.
Измерение параметра Херста подтверждают гипотезу о самоподобии – H=0.8.
Можно сделать следующие выводы: распределение Интернет трафика на магистральном узле провайдера Интернет близко к Пуассоновскому, но им не является. Поток данных является самоподобным. Близость распределения к Пуассоновскому можно объяснить наличием большого числа мультиплексированных потоков, так как объектом исследования является магистральная линия. Самоподобие можно расценивать как фундаментальное статистическое свойство сетевого трафика, которое необходимо учитывать на практике.
Практические результаты теории телетрафика используются в разных инженерных аспектах:
— Моделирование при проектировании, расчет пропускной способности;
— Качество обслуживания в сетях передачи данных (QoS);
— Выявление аномалий.
Существуют спектральные методы обнаружения аномалий в телетрафике.
Например, теория вейвлет-анализа трафика мультисервисных сетей.
Одной из составляющих классической модели сетевого ряда является периодическая составляющая гармонического типа, которая может быть описана конечным рядом Фурье, построенным по экспериментальным данным. В качестве альтернативы Фурье-анализу может использоваться вейвлет-анализ (анализ с помощью вейвлет-функций), позволяет узнать не только частотные характеристики ряда, но и локальные выбросы. Различают дискретный и непрерывный вейвлет-анализ, аппарат которых можно применять как для непрерывных, так и для дискретных сигналов.
автор:Елена Фельдман


